On this page

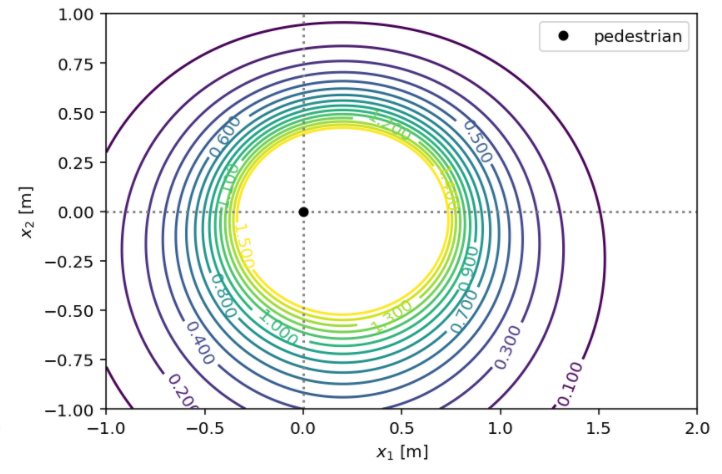
1D Wall

Parametric

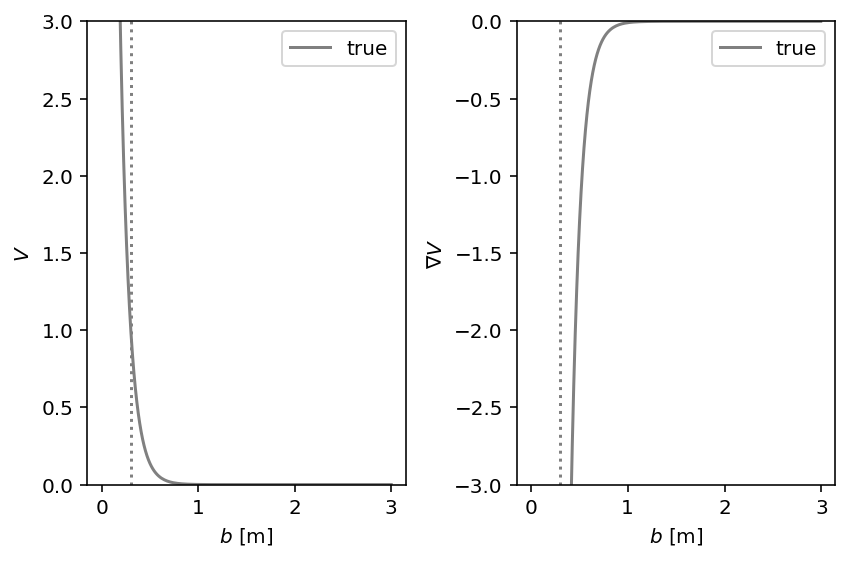
This is an extension of the 1D example to study the robustness of the inference process to potentials with steep gradients. We use a modified \(V(b)\) potential that could be described as a “soft wall” at \(b=\sigma\). The amount of gradients is determined by the width \(w\) of this wall:

(10)\[\begin{align} V(b) &= \exp\left(- \frac{b - \sigma}{w} \right) \end{align}\]

with its two parameters \(\sigma\) and \(w\).

ped_ped = socialforce.potentials.PedPedPotentialWall(w=0.1)
with socialforce.show.canvas(ncols=2) as (ax1, ax2): 
    ax1.set_ylim(0.0, 3.0)
    ax2.set_ylim(-3.0, 0.0)
    socialforce.show.potential_1d_parametric(
        ped_ped, ax1, ax2, 
        label=r'true', sigma_label=r'true $\sigma$', color='gray')
_images/pedped_1d_wall_2_0.png

Scenario

We generate a single Circle scenario.

circle = socialforce.scenarios.Circle(ped_ped=ped_ped)
scenario = circle.generate(1)
true_experience = socialforce.Trainer.scenes_to_experience(scenario)

with socialforce.show.track_canvas() as ax:
    socialforce.show.states(ax, scenario[0])
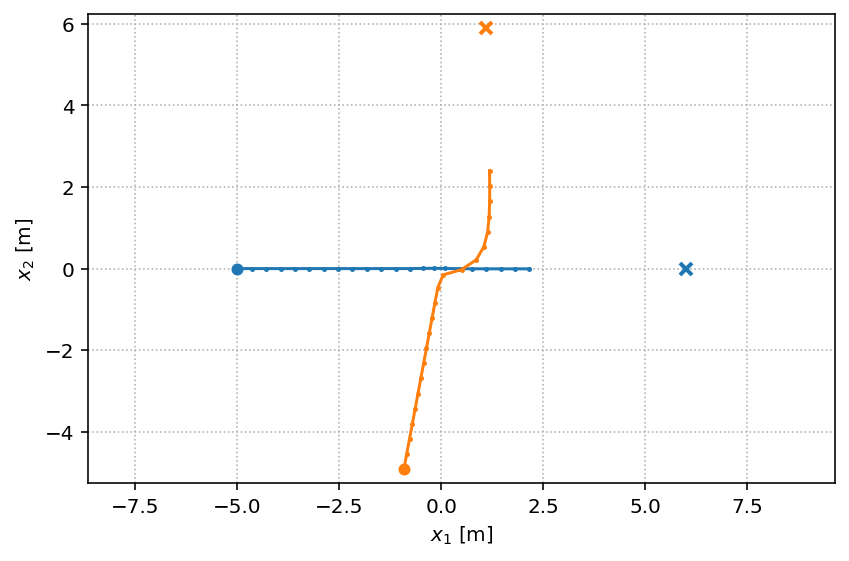
_images/pedped_1d_wall_4_0.png

This synthetic path shows a non-smooth direction change of the orange pedestrian. This is an artifact stemming from the finite step size in the simulation of the dynamics. We could remove this artifact by increasing the oversampling in our simulation.

MLP

We infer the parameters of an MLP to approximate the 1D scalar function \(\textrm{SF}(b)\) above from synthetic observations. The PedPedPotentialMLP is a two-layer MLP with softplus activations:

(11)\[\begin{align} \textrm{MLP}(b) &= \textrm{Softplus} \;\; L_{1\times5} \;\; \textrm{Softplus} \;\; L_{5\times1} \;\; b \end{align}\]

which is written in terms of linear and non-linear operators where the Softplus operator applies the softplus function on its input from the right and \(L\) is a linear operator (a matrix) with the subscript indicating the \(\textrm{output features} \times \textrm{input features}\). This two-layer MLP with 5 hidden units has 10 parameters.

V = socialforce.potentials.PedPedPotentialMLP(hidden_units=8)
initial_state_dict = copy.deepcopy(V.state_dict())

Inference

We use a standard optimizer from PyTorch (SGD). You can specify a standard PyTorch loss function for the Trainer as well but here the default of a torch.nn.L1Loss() is used.

simulator = socialforce.Simulator(ped_ped=V)
opt = torch.optim.SGD(V.parameters(), lr=3.0)
socialforce.Trainer(simulator, opt).loop(100, true_experience, log_interval=10)
final_state_dict = copy.deepcopy(V.state_dict())

epoch 10: 0.01935910070980234

epoch 20: 0.01923418208025396

epoch 30: 0.019103735252948745

epoch 40: 0.018915292507569705

epoch 50: 0.01855790857890887

epoch 60: 0.017838151094370654

epoch 70: 0.017187436377363547

epoch 80: 0.01637901269298579

epoch 90: 0.01500139628270907

epoch 100: 0.012028532202488609

# HIDE CODE
with socialforce.show.canvas(ncols=2) as (ax1, ax2):
    ax1.set_ylim(0.0, 3.0)
    ax2.set_ylim(-3.0, 0.0)

    socialforce.show.potential_1d_parametric(
        circle.ped_ped, ax1, ax2, 
        label=r'true $V_0 e^{-b/\sigma}$', sigma_label=r'true $\sigma$', color='gray')

    V.load_state_dict(initial_state_dict)
    socialforce.show.potential_1d(V, ax1, ax2, label=r'initial MLP($b$)', linestyle='dashed', color='C0')

    V.load_state_dict(final_state_dict)
    socialforce.show.potential_1d(V, ax1, ax2, label=r'MLP($b$)', color='C0')
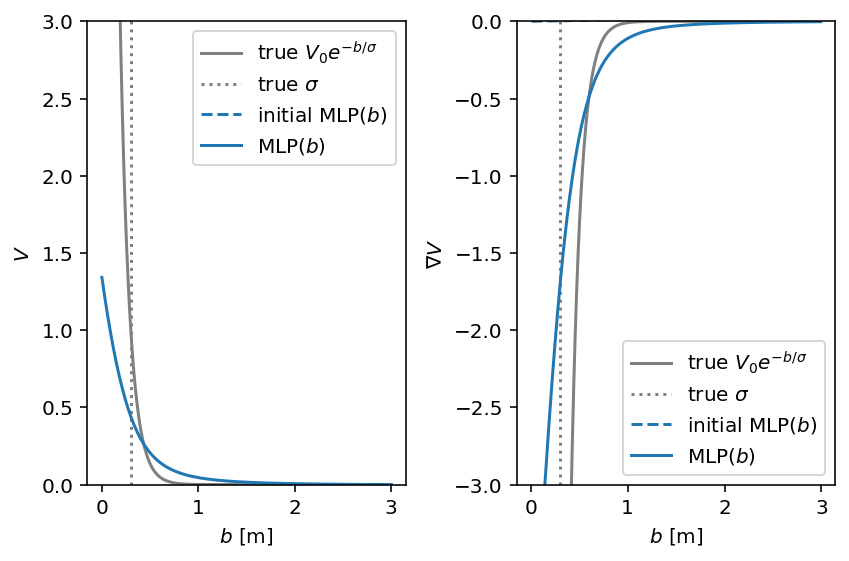
_images/pedped_1d_wall_10_0.png

We can see that the numerical challenges impact our ability to infer the parameters of this potential. When we reduce \(w\) further, this discrepancy grows.