On this page

Corridor

We want to qualitatively study the impact of non-standard Social Force potentials.

def initial_state_corridor(n):
    _ = torch.manual_seed(42)

    # first n people go right, second n people go left
    state = torch.zeros((n * 2, 6))

    # positions
    state[:n, 0:2] = ((torch.rand((n, 2)) - 0.5) * 2.0) * torch.tensor([25.0, 4.5])
    state[n:, 0:2] = ((torch.rand((n, 2)) - 0.5) * 2.0) * torch.tensor([25.0, 4.5])

    # velocity
    state[:n, 2] = torch.normal(torch.full((n,), 1.34), 0.26)
    state[n:, 2] = torch.normal(torch.full((n,), -1.34), 0.26)

    # x destination
    state[:n, 4] = 100.0
    state[n:, 4] = -100.0

    return state

initial_state = initial_state_corridor(60)

The space is just two walls at y=5.0m and y=−5.0m. To avoid boundary effects, the walls extend beyond the periodic boundaries at x=−25m and x=25m.

upper_wall = torch.stack([torch.linspace(-30, 30, 600), torch.full((600,), 5)], -1)
lower_wall = torch.stack([torch.linspace(-30, 30, 600), torch.full((600,), -5)], -1)
ped_space = socialforce.potentials.PedSpacePotential([upper_wall, lower_wall])

Reference Potential

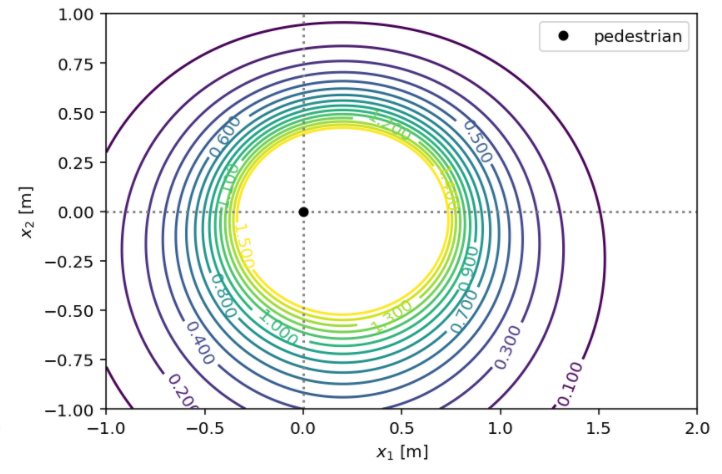
Standard SF:

ped_ped = socialforce.potentials.PedPedPotential()

# HIDE CODE
simulator = socialforce.Simulator(ped_ped=ped_ped, ped_space=ped_space,
                                  oversampling=2, delta_t=0.08)
simulator.integrator = socialforce.simulator.PeriodicBoundary(
    simulator.integrator, x_boundary=[-25.0, 25.0])

with torch.no_grad():
    states_sf = simulator.run(initial_state, 250)

with socialforce.show.track_canvas(ncols=2, figsize=(12, 2), tight_layout=False) as (ax1, ax2):
    socialforce.show.states(ax1, states_sf[0:1], monochrome=True)
    socialforce.show.space(ax1, ped_space)
    ax1.text(0.1, 0.1, '$t = 0s$', transform=ax1.transAxes)
    ax1.set_xlim(-25, 25)

    socialforce.show.states(ax2, states_sf[249:250], monochrome=True)
    socialforce.show.space(ax2, ped_space)
    ax2.text(0.1, 0.1, '$t = 20s$', transform=ax2.transAxes)
    ax2.set_xlim(-25, 25)
_images/corridor_7_0.png 
# HIDE CODE
with socialforce.show.track_canvas(figsize=(6, 2), tight_layout=False, show=False, dpi=130) as ax:
    ax.set_xlim(-25, 25)
    socialforce.show.space(ax, ped_space)
    video = socialforce.show.state_animation(ax, states_sf, delta_t=0.08).to_html5_video()

IPython.display.HTML(video)

Diamond Potential

ped_ped = socialforce.potentials.PedPedPotentialDiamond(sigma=0.5)

# HIDE CODE
simulator = socialforce.Simulator(ped_ped=ped_ped, ped_space=ped_space,
                                  oversampling=2, delta_t=0.08)
simulator.integrator = socialforce.simulator.PeriodicBoundary(
    simulator.integrator, x_boundary=[-25.0, 25.0])

with torch.no_grad():
    states_diamond = simulator.run(initial_state, 250)

with socialforce.show.track_canvas(ncols=2, figsize=(12, 2), tight_layout=False) as (ax1, ax2):
    socialforce.show.states(ax1, states_diamond[0:1], monochrome=True)
    socialforce.show.space(ax1, ped_space)
    ax1.text(0.1, 0.1, '$t = 0s$', transform=ax1.transAxes)
    ax1.set_xlim(-25, 25)

    socialforce.show.states(ax2, states_diamond[249:250], monochrome=True)
    socialforce.show.space(ax2, ped_space)
    ax2.text(0.1, 0.1, '$t = 20s$', transform=ax2.transAxes)
    ax2.set_xlim(-25, 25)
_images/corridor_11_0.png 
# HIDE CODE
with socialforce.show.track_canvas(figsize=(6, 2), tight_layout=False, show=False, dpi=130) as ax:
    ax.set_xlim(-25, 25)
    socialforce.show.space(ax, ped_space)
    video = socialforce.show.state_animation(ax, states_diamond, delta_t=0.08).to_html5_video()

IPython.display.HTML(video)

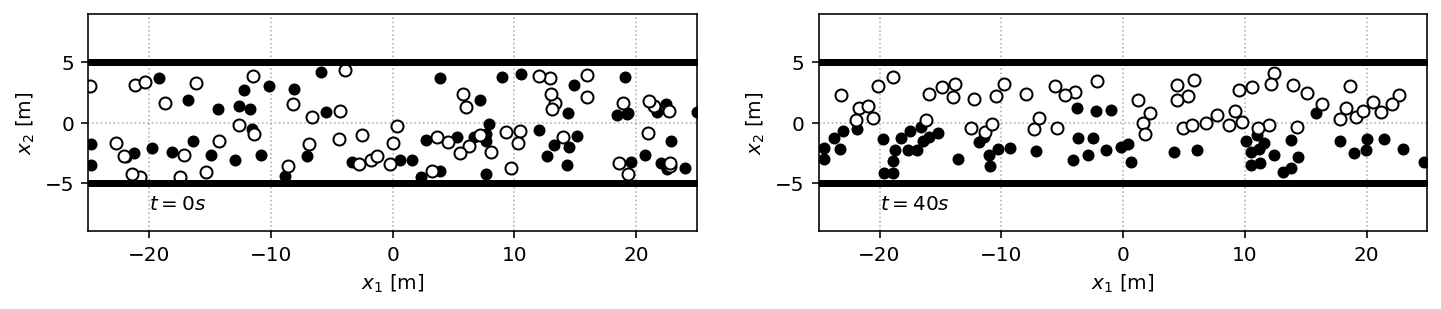
Asymmetric Diamond

ped_ped = socialforce.potentials.PedPedPotentialDiamond(sigma=0.5, asymmetry_angle=-20.0)

# HIDE CODE
simulator = socialforce.Simulator(ped_ped=ped_ped, ped_space=ped_space,
                                  oversampling=2, delta_t=0.08)
simulator.integrator = socialforce.simulator.PeriodicBoundary(
    simulator.integrator, x_boundary=[-25.0, 25.0])

with torch.no_grad():
    states_diamond_sd = simulator.run(initial_state, 500)

with socialforce.show.track_canvas(ncols=2, figsize=(12, 2), tight_layout=False) as (ax1, ax2):
    socialforce.show.states(ax1, states_diamond_sd[0:1], monochrome=True)
    socialforce.show.space(ax1, ped_space)
    ax1.text(0.1, 0.1, '$t = 0s$', transform=ax1.transAxes)
    ax1.set_xlim(-25, 25)

    socialforce.show.states(ax2, states_diamond_sd[499:500], monochrome=True)
    socialforce.show.space(ax2, ped_space)
    ax2.text(0.1, 0.1, '$t = 40s$', transform=ax2.transAxes)
    ax2.set_xlim(-25, 25)
_images/corridor_15_0.png 
# HIDE CODE
with socialforce.show.track_canvas(figsize=(6, 2), tight_layout=False, show=False, dpi=130) as ax:
    ax.set_xlim(-25, 25)
    socialforce.show.space(ax, ped_space)
    video = socialforce.show.state_animation(ax, states_diamond_sd, delta_t=0.08).to_html5_video()

IPython.display.HTML(video)

Speed Analysis

# HIDE CODE
def relative_speeds(states):
    speeds = np.linalg.norm(states[:, :, 2:4], axis=-1)
    preferred = states[:, :, 9]
    relative = speeds / preferred

    # ignore the first 50
    relative = relative[50:]
    return relative.reshape(-1)

def median_speed(states):
    speeds = np.linalg.norm(states[:, :, 2:4], axis=-1)

    # ignore the first 50
    speeds = speeds[50:]
    return np.median(speeds)

with socialforce.show.canvas() as ax:
    r_sf = relative_speeds(states_sf)
    r_diamond = relative_speeds(states_diamond)
    r_diamond_sd = relative_speeds(states_diamond_sd)
    ax.hist([r_sf, r_diamond, r_diamond_sd], bins=30, range=(0.8, 1.35), density=True, 
            label=[f'Social Force, $v_{{median}}$ = {median_speed(states_sf):.2f}m/s', 
                   f'diamond, $v_{{median}}$ = {median_speed(states_diamond):.2f}m/s',
                   f'speed-dependent diamond, $v_{{median}}$ = {median_speed(states_diamond_sd):.2f}m/s'])
    ax.legend()
    ax.set_xlabel('$v / v_{preferred}$ [m/s]')
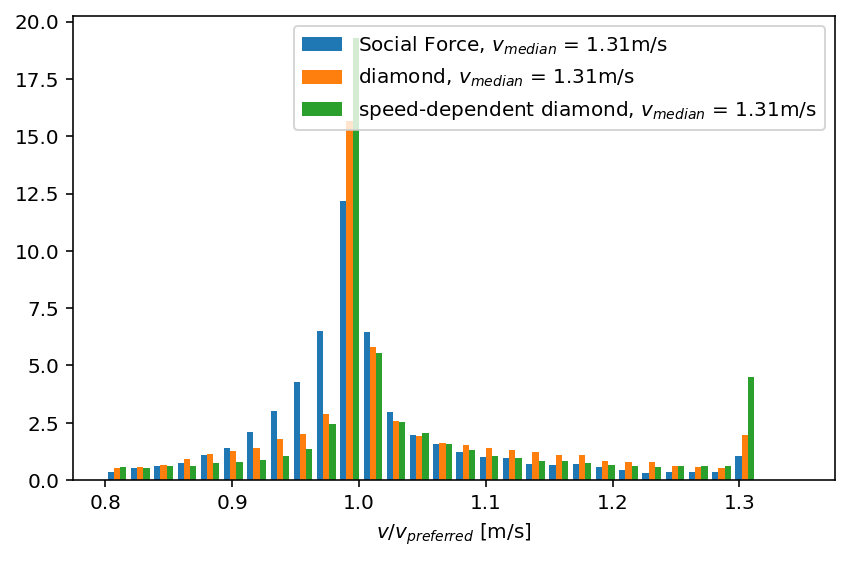
_images/corridor_18_0.png

The simulation with standard social force potential leads to pedestrians that are above their preferred speed whereas in the simulation with the diamond potential the median speed as at the preferred speed of 1.34m/s. This is a consequence of the asymmetric nature of the Social Force: the force experianced by pedestrian α due β is different (not just opposite) from the force experience by β from α. When pedestrian α walks in front of β, β will feel almost no force to slow down as the potential of α is shifted more towards the front. Pedestrian α however will be in the range of the potential from β who is behind. That force will be halfed by the field-of-view modulation, but that is still a stronger force than what β experiences.

In this corridor example with the Social Force pedestrian-pedestrian potential, pedestrians that are in front tend to get pushed to accelerate more than the pedestrians behind to slow down. There is no such asymmetry in the diamond potential.

Asymmetry Analysis

# HIDE CODE
def x2(states):
    x2_coordinates = np.copy(states[:, :, 1])
    x2_coordinates[states[:, :, 6] < 0.0] *= -1.0

    # only take last ones
    x2_coordinates = x2_coordinates[-1]
    return x2_coordinates.reshape(-1)

def mean_x2(states):
    return np.mean(x2(states))

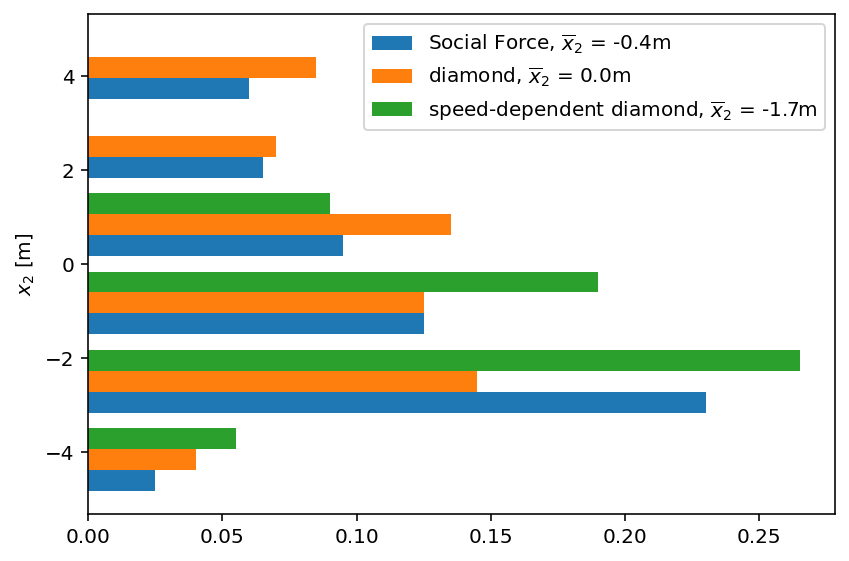
with socialforce.show.canvas() as ax:
    x2_sf = x2(states_sf)
    x2_diamond = x2(states_diamond)
    x2_diamond_sd = x2(states_diamond_sd)
    ax.hist([x2_sf, x2_diamond, x2_diamond_sd], bins=6, range=(-5.0, 5.0), density=True, 
            label=[f'Social Force, $\\overline{{x}}_2$ = {mean_x2(states_sf):.1f}m', 
                   f'diamond, $\\overline{{x}}_2$ = {mean_x2(states_diamond):.1f}m',
                   f'speed-dependent diamond, $\\overline{{x}}_2$ = {mean_x2(states_diamond_sd):.1f}m'],
            orientation='horizontal')
    ax.legend()
    ax.set_ylabel('$x_2$ [m]')
_images/corridor_21_0.png